برای هر x عضو دامنه برقرار است. لذا این عبارت جبری یک اتحاد است، اما تساوی
فقط برای x=1 برقرار است. پس این عبارت یک اتحاد نمی باشد. در واقع در مورد یک اتحاد در اصل به یک تساوی بدیهی چون 0=0 می رسیم. دو طرف ساده شده و تساوی 0=0 حاصل می شود. 
باشد آنگاه داریم:
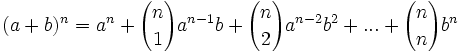
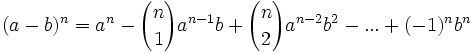
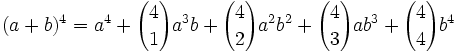
انتگرالها یک بحث اساسی ریاضیات عالی را تشکیل داده که می‌توان کاربرد آنرا درتمام علوم طبیعی، انسانی وغیره مورد مطالعه قرارداد.
اولین بار لایب نیتس نماد استانداردی برای انتگرال معرفی کرد. 
aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال‌پذیر است و dx نمادی برای متغیر انتگرال گیری است.
از لحاظ تاریخی dx یک کمیت بی نهایت کوچک را نشان می‌دهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی پایه گذاری شده است.
تابع اولیه
هر گاه معادله مشتق تابعی معلوم باشد وبخواهیم معادله اصلی تابع را تعیین کنیم این عمل را تابع اولیه می نامیم.
تعریف: تابع اولیه y = f(x)را تابعی مانند Y = F(x) + c می نامیم،هرگاه داشته باشیم:
cعدد ثابت (y = F(x) + c)" = y = f(x)
تعریف:هرگاه معادله دیفرانسیلی تابعی معلوم باشد وبخواهیم معادله اصلی تابع را معلوم کنیم این عمل راانتگرال نا معیین نامیده و آن را با نماد 
نمایش می‌دهند.
بنا به تعریف نماد
را انتگرال نامعین نامیده وحاصل آن را تابعی مانندF(x) + c در نظر میگیریم هر گاه داشته باشیم: 
با شرط: (F(x) + c)" = f(x)
بنا به تعریف نماد
را انتگرال معین نامیده و حاصل آن را عددی به صورت زیر تعریف می‌کنیم: a<x<b ![\int_a^b f(x).dx=[F(x)]_a^b=F(b)-F(a)](http://upload.wikimedia.org/math/a/4/9/a496f4d22ac72fe3e47d598b6e5c56dc.png){kind=small}
aوb را به ترتیب کرانهای بالا و پایین انتگرال مینامیم.
اگر تابعی دارای انتگرال باشد به آن انتگرال‌پذیر گویند.
از نظر هندسی انتگرال برابر است با مساحت سطح محصور زیر نمودار.
نکته انتگرال نمودار سه بعدی(انتگرال دو گانه)معرف حجم محصور زیر نمودار است و انتگرال سه‌گانه معرف پارالل زیر نمودار است(غیرقابل تصور).
انتگرال یک تابع مثبت پیوسته در بازه (0,10) در واقع پیدا کردن مساحت محصور بین خطوط x=0 , x=10 و خم منحنی fx است. aو b نقاط ابتدا و انتهای بازه هستند و f تابعی انتگرال‌پذیر است و dx نمادی برای متغیر انتگرال گیری است.
انتگرال یک تابع مساحت زیر نمودار آن تابع است.
(محاسبه انتگرال) انتگرال گیری به معنی محاسبه سطح زیر نمودار با استفاده از روشها وقوانین انتگرال گیری است.
از مهم‌ترین تعاریف در انتگرال می‌توان از انتگرال ریمان و انتگرال لبگ (Lebesgue) است. انتگرال ریمان به‌وسیله برنهارد ریمان در سال 1854 ارائه شد که تعریف دقیقی را از انتگرال ارائه می‌داد تعریف دیگر را هنری لبگ ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه می‌کرد. از دیگر تعاریف ارائه شده در زمینه انتگرال می‌توان به انتگرال ریمان-استیلچس (Riemann-Stieltjes) اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهم‌ترین تعاریف انتگرال می باشند:
انتگرال ها در واقع مساحت محصور در زیر نمودار هستند و در فیزیک می‌توان برای کاربرد های زیادی تعریف کرد مانند کار انجام شده در یک فر آیند ترمودینامیکی از انتگرال رابطه فشار و حجم به دست می‌آید. اما به طور کلی می‌توان آن را تغییرات کمیت حاصل ضرب افقی و عممودی نمودار نامیدمثلا: در یک رابطه کمیت ها را تحلیل ابعادی می کنیم مثلا رابطه سرعت و زمان را به صورت زیر نوشته می‌شود:
![v=[L]/[T] t=[T] \!](http://upload.wikimedia.org/math/8/2/2/822905b570a5c6ea0f79e5f228645e54.png){kind=small}
سپس دو تحلیل را در هم ضرب می کنیم:
![[L] \!](http://upload.wikimedia.org/math/b/2/6/b2600468c360b80f3b363f56c4ddd214.png){kind=small}
پس مساحت محصور در زیر نمودار برابر با تغییرات طول (جابجایی) است.
|
سرپرست تیم فوتبال استقلال با بیان اینکه این تیم برای حضور در لیگ قهرمانان آسیا نیاز به تقویت دارد، گفت: برای تقویت برخی پست ها باید بازیکن بگیریم. |
 |
|
|
||
|
منصور پورحیدری در پایان تمرین امروز آبی پوشان ضمن بیان این مطلب افزود: استقلال توانسته با تمرینات منظمی که انجام می دهد خود را به صدر جدول نزدیک کرده و آرام آرام برای رسیدن به رده نخست جدول برنامه‌های خود را آماده کرده است. پورحیدری ادامه داد: این طبیعی است که تیم‌ها در ابتدای فصل تا حدودی ناهماهنگ هستند اما هر چه از شروع مسابقات می گذرد بازیکنان به مرز آمادگی رسیده و بازی‌های بهتری از خود ارائه می دهند. سرپرست تیم فوتبال استقلال در مورد وضعیت مصدومان این تیم گفت: در حال حاضر میلاد میداودی و محمد محمدی از مصدومین اصلی ما به شمار می روند. متاسفانه میداوودی در دیدار مقابل ملوان بندرانزلی دچار مصدومیت شدیدی شد که فکر می کنم تا سه ماه نمی تواند تیم استقلال را همراهی کند اما محمد محمدی با زحمات کادر پزشکی و انجام مراقبت‌های ویژه خیلی زود به جمع ما ملحق خواهد شد. وی در خصوص وضعیت دیگر مصدومان تیم استقلال نیز گفت: خوشبختانه فرهاد مجیدی، محسن یوسفی و مجتبی جباری و همچنین فرزاد آشوبی تمرینات گروهی خود را با تیم شروع کرده‌اند و فکر می کنم طی چند روز آینده بتوانند برای تیم استقلال بازی کنند. حضور این بازیکنان در تمرینات گروهی روحیه دیگر بازیکنان نیز بالا برده و انگیزه بازیکنان نسبت به گذشته بیشتر شده است. پورحیدری در خصوص حضور مجید نامجو مطلق در کادر فنی تیم استقلال نیز پاسخ داد: نامجومطلق از بازیکنان بزرگ و از قدیمی‌های استقلال است. در ابتدای فصل پرویز مظلومی با نامجومطلق صحبت کرد اما وی حاضر نشد که به استقلال بازگردد اما صحبت‌هایی که در این چند روز در خصوص حضور وی در استقلال مطرح شده، اصلا صحت نداشته و هیچ صحبتی نیز بین ما و مجید نامجو مطلق انجام نگرفته است و قطعا حضور ایشان در استقلال منتفی است. وی اشاره ای نیز به حضور خود در تیم همیاری اراک داشت و افزود: مسئولان تیم همیاری اراک به من خیلی محبت دارند، خصوصا معاونت استانداری استان مرکزی که مردی علاقه‌مند به ورزش است. من با توجه به ارتباطی صمیمی که با ایشان دارم هر کاری که از دستم بر بیاید حتی در حد مشاوره و شاید حضور فیزیکی در اراک برای تیم همیاری انجام خواهم داد تا این تیم بتواند در مسابقات موفق ظاهر شود. سرپرست تیم فوتبال استقلال تهران در پایان پیرامون وضعیت نقل و انتقال این تیم در نیم فصل نیز پاسخ داد: جذب بازیکن بستگی به نیاز تیم دارد با توجه به حضور استقلال در جام باشگاه های آسیا قطعا ما نیاز به تقویت بعضی از خطوط تیم خود داریم که البته گرفتن بازیکن بستگی به نظر سرمربی تیم داشته و وی باید نیازهای خود را به ما اعلام کرده تا ما هر چه سریعتر بازیکنان مورد نظر را جذب کنیم. |
